?We have a wide variety of research interests including
See below for a brief description of each of these areas and available postgraduate projects.
A full list of publications of members of the group can be found here.
Gravitational waves are dynamical distortions of spacetime, predicted by Einstein's theory of general relativity. Though they have never been directly observed (they are very weak), they are created whenever massive bodies accelerate. Numerous new experiments hope to use these signals to observe exotic processes in the universe, such as black hole mergers, and test theories of gravity.
We are involved in numerical modelling of strong sources of gravitational waves, most notably black hole and neutron star binaries. This work involves casting the Einstein equations in the form of an evolution system, which we implement in a computer code. From our models we are able to determine the dynamics of the spacetime, such as the evolution of black hole event horizons, and the emitted gravitational waves. We are using these results to develop new predictions about black hole astrophysics, comparing with analytical results, and building gravitational wave templates to aid detecting them by experiment.
Partial Differential Equations (3rd year)
Cosmology is the study of the large scale structures of spacetime and the origin and evolution of our Universe. The standard model of cosmology is now well established, but the natures of Dark Matter and Dark Energy remain unknown and are among the most important theoretical issues of modern physics. At Rhodes University, we are mostly involved in testing the Cosmological principle, either by studying the Copernican principle, or the averaging/backreaction issue. We also study modification of gravity in order to probe the validity of the equivalence principle on astrophysical and cosmological scales. Our work concentrates on theoretical modelisations and predictions. These studies are an important step in understanding the geometry of the Universe on the large scales in greater details, in order to prepare the way for future observations such as those of EUCLID or the SKA.
The equations governing black holes, neutron stars and cosmological scenerios like the big bang, can not be solved analytically on paper and pencil. Instead, we study these system using large-scale computer models which incorporate as much of the physical scenerios as possible: general relativity, maxwell equations, fluid dynamics, etc.![Binary black holes [AEI/Benger].](/media/rhodesuniversity/content/mathematics/images/gravity/B7_bbh-200x200.jpg)
Our group is a leading collaborator in developing one of the primary computing codes used to model relativistic astrophysics for a diverse set of projects ranging from binary black hole evolutions, to supernova core collapse. The Llama evolution code incorporates an implementation of the Einstein evolution equations and is coupled to a matter model. The code is parallelized to run efficiently on high-performance computing architectures and large cluster computers. Research in this area ranges over a wide range of disciplines, including developing new numerical schemes, improved reformulations of the evolution equations and gauges, and new analysis tools to help understand and visualize the results of models. A particularly active project at Rhodes involves developing new schemes for modelling gravitational waves through a characteristic formulation of the Einstein equations.?
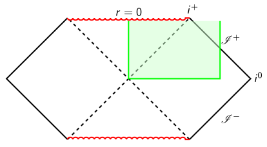
Mathematical general relativity ties fundamental problems of gravitational physics with beautiful questions in mathematics. The object is the study of manifolds equipped with a Lorentzian metric satisfying the Einstein field equations. Due to the broad scope of questions one can ask about the physics, many different areas of mathematics are employed such as group theory, topology, differential geometry and partial differential equations.
Our groups main focus is on
Last Modified: Sun, 16 Feb 2020 15:56:25 SAST